Trazado de líneas
Diferentes tipos de líneas y situaciones en que se dibujan se resuelven con técnicas diferentes.
- Líneas cortas, o líneas que corren paralelas a otras que nos sirven de referencia.
- Líneas largas. Es el caso de líneas que unen dos puntos alejados, sin ninguna otra referencia. Las primeras líneas de cualquier croquis entran en esta categoría.
Líneas cortas o líneas paralelas a otras ya existentes se las puede dibujar de un solo trazo. Primero se deben mirar bien los puntos de inicio y terminación para luego ejecutar el trazo.
Para el trazado de líneas largas vamos a dar tres técnicas que se utilizarán según las circunstancias.
Líneas punto a punto
La técnica más rápida es, una vez determinados los puntos a unir se comienza moviendo el lápiz desde uno de ellos hacia el otro. Mientras se hace este movimiento se debe mantener la vista sobre el punto de destino. Esto último nos permitirá conservar la dirección.
Líneas compuestas
Una segunda técnica es proceder mediante trazos de cinco a siete centímetros; como si se estuviesen dibujando una sucesión de líneas más cortas. La interrupción del trazo permite verificar el rumbo del trazo y se corregir si es necesario. Los trazos sucesivos no se superponen a fin de posibilitar uniformidad de espesor. Se deja una pequeñísima luz entre ellos de forma tal que apenas resulte perceptible la interrupción y mantenga el espesor uniforme. [dibujo de ejemplo].
Líneas de construcción
Una tercera técnica, particularmente aplicable cuando se está planteando el dibujo, es utilizar líneas de tanteo. Resulta un poco más lenta que las anteriores, pero es de gran ayuda para obtener líneas rectas particularmente cuando son muy largas. Consiste en insinuar la línea en forma apenas visible con trazos muy suaves. Idealmente, solo el dibujante debería percibir esos trazos de tanteo. Se observa el resultado obtenido. Se introducen las correcciones necesarias hasta lograr definir el trayecto correcto. Entonces se comienza el trazado de la línea en forma similar al primer método, pero ahora con una guía visual. Si fuese necesario, porque se utilizaron demasiadas líneas de tanteo, se podrán borrar las que no sirven, antes del trazado definitivo.
Linea Recta:
En geometría euclidiana, la recta o la línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, es decir, no posee principio ni fin.
Algoritmo de Bresenham para trazar líneas
El algoritmo de Bresenham es un algoritmo creado para dibujar rectas en los dispositivos de gráficos rasterizados, como por ejemplo un monitor de ordenador, que determina qué pixeles se rellenarán, en función de la inclinación del ángulo de la recta a dibujar.
Es un algoritmo preciso para la generación de líneas de ratreo que convierte mediante rastreo las líneas al utilizar solo cálculos incrementales con enteros que se pueden adaptar para desplegar circunferencias y curvas. Los ejes verticales muestran las posiciones de rastreo y los ejes horizontales identifican columnas de pixel.
Si 0<|m|<1
*Se capturan los extremos de la línea y se almacena el extremo izquierdo en (x0,y0).
*Se carga (x0,y0) en el bufer de estructura (se traza el primer punto)
*Se calculan las constantes Δx,Δy, 2Δy y 2Δy-Δx y se obtiene el valor inicial para el
parametro de decisión p0=2Δy-Δx.
Para j=0 mientras j<Δx
*En cada xk a lo largo de la línea, que inicia en k=0 se efectúa la prueba siguiente:
Si pk<0
*Trazamos (xk+1,yk).
*Asignamos pk+1= pk+2Δy.
Sino
*Trazamos (xk+1,yk+1).
*Asignamos pk+1= pk+2Δy-2Δx.
Fin Para
Si |m|>1
*Recorremos la dirección en pasos unitarios y calculamos los valores sucesivos
de x que se aproximen más a la trayectoria de la línea.
2.2 REPRESENTACIÓN Y TRAZOS DE
POLINOMIOS
Representación de los polígonos
Polígono es la superficie plana encerrada dentro de un contorno formado por segmentos rectos unidos en sus extremos.
- Cada uno de los segmentos se denomina lado.
- El punto de unión de cada par de segmentos se denomina ángulo.
- El numero de lados, ( y por tanto de ángulos) ha de ser mayor o igual a tres.
Elementos de un polígono
Son los segmentos que lo limitan.
Vértices
Son los puntos donde concurren dos lados.
Ángulos interiores de un polígono
Son los determinados por dos lados consecutivos.
El polígono es el caso bidimensional del politopo, figura geométrica general definida para cualquier número de dimensiones. a noción geométrica elemental ha sido adaptada de distintas maneras para servir a propósitos específicos.
En Matemáticas, un politopo regular es una figura geométrica con un alto grado de simetría. Ejemplo de politopos regulares en dos dimensiones son el cuadrado, el pentágono y el hexágono regular.
La representación básica de alguna imagen se limita a polígonos regulares e irregulares formados por vértices.
Se pueden organizar los polígonos para mejorar el tratamiento.
Ahora que se ha aclarado el concepto y los elementos básicos de un polígono y su generalización (politopo) podemos centrarnos en la construcción de polígonos en algún ambiente de graficación.
Dibujando Poligonos con OpenGL
OpenGL tiene únicamente unas pocas primitivas geométricas: puntos, líneas, polígonos. Todas ellas se describen en términos de sus respectivos vértices. Un vértice está caracterizado por 2 o 3 números en como flotante, las coordenadas cartesianas del vértice, (x, y) en 2D y (x, y, z) en 3D. Aunque las coordenadas cartesianas son las más comunes, en gráficos por ordenador también existe el sistema coordenado homogéneo en el que cada punto se describe con 4 números en coma flotante (x, y, z, w). Volveremos a él después de ver algunas nociones elementales de trazado en 3D.
Como en OpenGL todos los objetos geométricos son finalmente descritos como un conjunto ordenado de vértices.
2.3 TRANSFORMACIÓN BIDIMENCIONAL
*Con los algoritmos de primitivas ya podemos dibujar en pantalla
*El siguiente paso consiste en permitir modificar o manipular dichas primitivas
Transformaciones Geométricas
– Para poder implementar aplicaciones de diseño
– Para poder realizar animaciones
– Para interactuar con la escena
• Las transformaciones básicas que se necesitan son:
– Traslación: cambios en la posición
– Rotación: cambios en la orientación
– Escalado: cambios en el tamaño
Traslación
Una traslación es el movimiento en línea recta de un objeto de una posición a otra.
Se traslada cada punto P(x,y) dx unidades paralelamente al eje x y dy unidades paralelamente al eje y, hacia el nuevo punto P'(x',y').
Las ecuaciones quedan:
Si se definen los vectores columna queda:
Entonces la ecuación 1 puede ser expresada como:
Una forma de efectuar la traslación de un objeto es aplicándole a cada punto del mismo la ecuación 1. Para trasladar todos los puntos de una línea, simplemente se traslada los puntos extremos.
En la figura se muestra el efecto de trasladar un objeto 3 unidades en x y -4 unidades en y.
Esto se cumple también para el escalamiento y la rotación.
Escalamiento
Una transformación para alterar el tamaño de un objeto se denomina escalación.
Dependiendo del factor de escalación el objeto sufrirá un cambio en su tamaño pasando a ser mayor, o menor en su segmento de longitud.
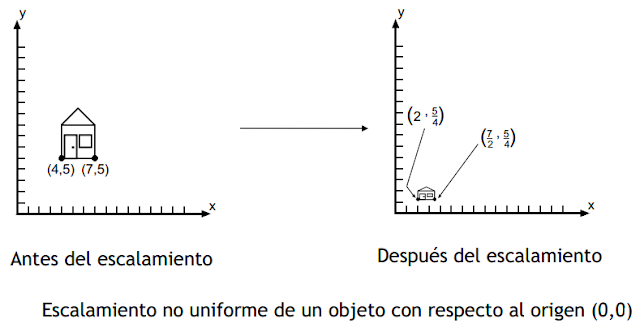
El escalamiento se hace con un factor sx en el eje x y en un factor sy en el eje y.
Escalamiento uniforme sx = sy
Escalamiento diferencial.
La transformación de escalamiento puede expresarse con las siguientes multiplicaciones
En forma matricial
Rotación
Para rotar un objeto (en este caso bidimensional), se ha de determinar la cantidad de grados en la que ha de rotarse la figura. Para ello, y sin ningún tipo de variación sobre la figura, la cantidad de ángulo ha de ser constante sobre todos los puntos.
Los puntos también pueden ser rotados un ángulo θ con respecto al origen
En forma matricial
2.4 REPRESENTACIÓN MATRICIAL
En las aplicaciones de diseño y de creación de imágenes, realizamos traslaciones, rotaciones y escalaciones para ajustar los componentes de la imagen en sus posiciones apropiadas. En este tema consideramos cómo se pueden volver a formular las representaciones de la matriz de modo que se pueden procesar de manera eficiente esas secuencias de transformación. Es posible expresar cada una de las transformaciones básicas en la forma de matriz general con las posiciones de coordenadas P y P’ representadas como columnas de vector.
Con las representaciones de matriz podemos establecer una matriz para cualquier
secuencia de transformaciones como una matriz de transformación compuesta al
calcular el producto de la matriz de las transformaciones individuales. La creación de
productos de matrices de transformación a menudo se conoce como
concatenación o composición de matrices.
- Traslaciones
de coordenadas P, la localización transformada final P, la localización transformada final
P’ se calcula como: P'=T(t x2,t2)·T(tx1,ty1)·P}{=T(tx2, 2)·T(t x1,t y1)}{·P
Donde se representan P y P’ como vectores de columna de coordenadas
homogéneas. Podemos verificar este resultado al calcular el producto de la matriz
para las dos agrupaciones asociativas. Asimismo, la matriz de transformación
compuesta para esta secuencia de transformaciones.
- Rotaciones
P'=R(θ2)·R(θ1){·P}=R(θ2){· (θ1)}·P
Al multiplicar las dos matrices de rotación, podemos verificar que dos rotaciones
sucesivas son aditivas
- Escalamiento
La siguiente figura ilustra una secuencia de transformación para producir escalación
con respecto de una posición fija seleccionada (xf,f) al utilizar una función de escalación
que sólo puede escalar en relación con el origen de las coordenadas
La multiplicación de matrices es asociativa. Para tres matrices cualesquiera A, B y C,
el producto matricial A·B·C se puede llevar a cabo al multiplicar primero a por B o
multiplicar primero B por C:2.35.A · BC=( A· B)·C =A·( B·C)
Por tanto, podemos evaluar los productos matriciales al utilizar una agrupación asociativa
ya sea de izquierda a derecha o de derecha a izquierda. Por otro lado, los productos
de la transformación tal vez no sean conmutativos. En general el producto matricial A·B
no es igual que B·A. Esto significa queremos trasladar y girar un objeto, debemos tener
cuidado sobre el sentido en que se evalúa la matriz compuesta.
2.5 VENTANA Y PUERTO DE VISIÓN
COLOCACIÓN DE VENTANAS Y RECORTE
Los programas de aplicaciones definen imágenes en un sistema de coordenadas mundiales.
Este puede ser cualquier sistema de coordenadas Cartesianas que un usuario halle conveniente.
Las imágenes definidas en coordenadas mundiales son procesadas por el sistema de graficas en
coordenadas de dispositivo. Comúnmente, un paquete de graficas permite a un usuario especificar qué
área de la definición de la imagen se desplegara y donde se colocara en el dispositivo de despliegue.
Podría elegirse una sola área para el dispositivo de despliegue o bien podrían seleccionarse varias áreas.
Estas áreas pueden colocarse en localidades aparte del despliegue o bien un área puede servir como
una pequeña inserción en un área mayor. Este proceso de transformación implica operaciones
para trasladar y escalar áreas seleccionadas y para borrar partes de la imagen que estén fuera de las
áreas.Estas operaciones se conocen como colocación de ventanas y recorte.
Transformación a la ventana de visión
• La escena se almacenan según un sistema de coordenadas reales (metros, cm, pulgadas)
• El usuario verá en cada momento una subárea de la escena, o varias simultáneamente
• Cada subárea se mapeará en zonas distintas de la pantalla
• La pantalla viene definida por un sistema de coordenadas enteras (pixels)
• Hay que transformar de un sistema a otro
CONCEPTOS DE COLOCACIÓN DE VENTANAS
El área rectangular en el dispositivo de despliegue en el cual se coloca la ventana se llama puerta de visión.
La figura 1 ilustra el trazo o planimetría de la selección de una imagen que queda dentro del área de
ventana en una puerta de visión designada. Esta planimetría se llama transformación de la visión o
bien transformación de normalización.
CONCLUSIÓN
este tema es muy interesante ya que nos explica las transformaciones que se pueden
llevar a cabo en nuestras imagenes las cuales pueden tener tres tipos de transformaciones
como los son:
– Traslación: cambios en la posición
– Rotación: cambios en la orientación
– Escalado: cambios en el tamaño
BIBLIOGRAFIA
http://graficacion-suirot18.blogspot.mx/2013/09/24-representacion-matricial.htm
http://graficacionito.blogspot.mx/2013/09/22-representacion-y-trazo-de-poligonos.html
http://inggraficacion.blogspot.mx/p/25-ventana-y-puerto-de-vision.html
http://graficacion-suirot18.blogspot.mx/2013/09/23-transformacion-bidimensional.html
http://serdis.dis.ulpgc.es/~ii-fgc/Tema%203%20-%20Transformaciones%202D.pdf
http://graficacionito.blogspot.mx/2013/09/22-representacion-y-trazo-de-poligonos.html
http://inggraficacion.blogspot.mx/p/25-ventana-y-puerto-de-vision.html
http://graficacion-suirot18.blogspot.mx/2013/09/23-transformacion-bidimensional.html
http://serdis.dis.ulpgc.es/~ii-fgc/Tema%203%20-%20Transformaciones%202D.pdf







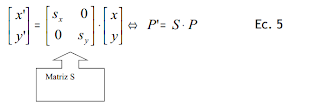


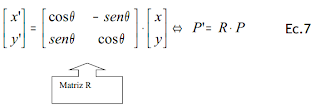




No hay comentarios:
Publicar un comentario