UNIDAD 3
3.1 REPRESENTACIÓN DE OBJETOS EN TRES DIMENSIONES
El diseño ayudado por ordenador representa un gran ahorro de esfuerzo y tiempo. Además
se consiguen resultados extraordinarios con respecto a los procedimientos clásicos de
diseño. Los programas de diseño industrial o arquitectónico admiten tres maneras de
representación de objetos.
se consiguen resultados extraordinarios con respecto a los procedimientos clásicos de
diseño. Los programas de diseño industrial o arquitectónico admiten tres maneras de
representación de objetos.
- Modelos bidimensionales del objeto o parte de él.
modificados. Normalmente se utiliza una representación formal del objeto, obteniendo sus
vistas desde diferentes puntos de visualización. Se denominan vistas principales de un
objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de
cubo.
objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de
cubo.
También se podría definir las vistas como, las proyecciones ortogonales de un
objeto, según las distintas direcciones desde donde se mire. Si situamos un observador
según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles
de un objeto.
objeto, según las distintas direcciones desde donde se mire. Si situamos un observador
según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles
de un objeto.
- Modelos tridimensionales que incluyan únicamente un conjunto de puntos
y líneas en el espacio.
representado rota en diferentes ángulos para su estudio o transformación definitiva.
Existen varias formas de representación en modo wireframe:
representado rota en diferentes ángulos para su estudio o transformación definitiva.
Existen varias formas de representación en modo wireframe:
- Representación alambrica: Activa este modo de sombreado.
- Representación alambrica det: Se muestran bordes alámbricos e iluminación
- Área de trabajo: Muestra los objetos como área de trabajo solamente.
completamente un objeto.
- Modelos sólidos que incluyen el dibujo de superficies y son los más completos y
- Suavizado + Resaltes: Activa este modo de sombreado, que permite
presentar mapas en la superficie de objetos.
Esto sucede mapa a mapa, pero puede presentar tantos mapas
como desee simultáneamente en el visor.
Los mapas sólo aparecen en objetos que tienen coordenadas
de mapeado.
- Suavizado: Muestra suavizado, pero no resaltes
Espacio tridimensional
El espacio 3D es un espacio matemático virtual creado por el programa de diseño 3D.
Este espacio está definido por un sistema cartesiano de tres ejes: X, Y, Z.
El punto donde salen las líneas virtuales que definen los ejes se llama origen y sus
coordenadas son (0, 0, 0). En este espacio virtual se crean, modifican y disponen los
diferentes objetos tridimensionales que van a componer la escena.
Este espacio está definido por un sistema cartesiano de tres ejes: X, Y, Z.
El punto donde salen las líneas virtuales que definen los ejes se llama origen y sus
coordenadas son (0, 0, 0). En este espacio virtual se crean, modifican y disponen los
diferentes objetos tridimensionales que van a componer la escena.
Fundamentos básicos del modelado en 3D
El 3D es una mera representación de coordenadas, que conforman estructuras envueltas
por una textura.
por una textura.
Por tanto, primero se deben construir un modelo, para ello hay técnicas de modelado
comunes, en las cuales se encuentran:
comunes, en las cuales se encuentran:
- 1. Estructuras Predefinidas: Aquellas estructuras ya armadas por el sistema.
tetera y plano.
Primitivas Extendidas: hedra, nudo toroide, caja "redondeada", cilindro
"redondeado" tanque de aceite, capsula, sprindle, forma L,
gengon, forma c, anillo ondulado, hose, prisma.
Primitivas Extendidas: hedra, nudo toroide, caja "redondeada", cilindro
"redondeado" tanque de aceite, capsula, sprindle, forma L,
gengon, forma c, anillo ondulado, hose, prisma.
Librerías: son formas armadas, disponibles en 3d Max 7; puertas,
ventanas, árboles, escaleras.
El renderizado es un proceso de cálculo complejo desarrollado por un ordenador destinado a
generar una imagen 2D a partir de una escena 3D. Así podría decirse que en el proceso de
renderización, la computadora "interpreta" la escena 3D y la plasma en una imagen 2D.
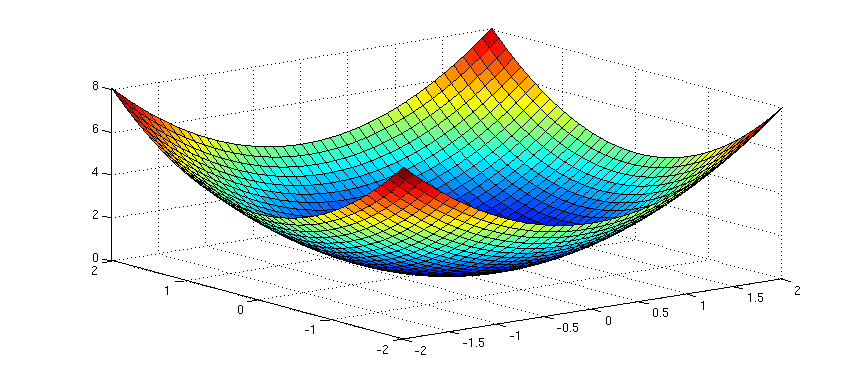
Una superficie es una extensión en que se consideran sólo dos dimensiones.
SUPERFICIES CURVAS
Las superficies curvas pueden generarse a partir de un conjunto funciones matemáticas que definen la superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario.
Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y gráfica posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones.
Es la mas conocida desde que nos ensenaron a utilizar las coordenadas cartesianas para graficar funciones.
En 3D, para representar una curva se requieren dos ecuaciones:
y = f (x), z = g(x)
Obteniendo una superficie en 3D que será:
z = f (x, y)
Representación Implícita
Para curvas y superficies estándar (rectas, círculos, planos, toroides, etc.), este tipo de definición es mas directa y permite visualizar y modificar sencillamente parámetros importantes y específicos de cada curva (radio en un circulo, distancia al origen en un plano, etc.).
En 3D, una superficie se describe por
f(x, y, z) = 0
Ejemplo
• Una esfera: x2 + y2 + z2 – r2 = 0
• Una curva corresponde a la intersección de dos superficies:
f(x, y, z) = 0 y g(x, y, z) = 0
Nota: el punto (x, y, z) debe pertenecer a ambas superficies.
Representación Paramétrica
El valor de cada variable espacial se expresa en términos de una variable independiente (t), llamada parámetro.
Estas funciones juntas han de formar las ecuaciones paramétricas de una curva:
x = x(t)
y = y(t)
z = z(t)
Cada valor de t determina un punto (x,y) que se puede representar en un sistema de coordenadas.
Superficie Paramétrica al conjunto de puntos (x,y,z,) dados por r(u,v)= x(u,v)i + y(u,v)j + z(u,v)k.
Las Ecuaciones x=(u,v), y=(u,v) y z=(u,v) se llaman Ecuaciones Paramétricas de la superficie.
BIBLIOGRAFIA
- 2. Box Modeling: Como su nombre lo indica, es el modelado de figuras complejas a
través de una caja. Empleando un modificador de mallas, Edith Mesh,
podrán ir extendiendo la caja, convirtiéndola en otra cosa.
de aspecto orgánico ó curvado, que emplea como punto de partida splines
para mediante diversos métodos, crear la malla 3d anidando los splines.
Renderizado
El renderizado es un proceso de cálculo complejo desarrollado por un ordenador destinado a
generar una imagen 2D a partir de una escena 3D. Así podría decirse que en el proceso de
renderización, la computadora "interpreta" la escena 3D y la plasma en una imagen 2D.
La renderización se aplica a los gráficos por ordenador, más comúnmente a la infografía.
En infografía este proceso se desarrolla con el fin de imitar un espacio 3D formado por
estructuras poligonales, comportamiento de luces, texturas, materiales, animación, simulando
ambientes y estructuras físicas verosímiles, etc. Una de la partes más importantes de los
programas dedicados a la infografía son los motores de render los cuales son capaces de
realizar técnicas complejas como radiosidad, raytrace (trazador de rayos), canal alpha,
reflexión, refracción, iluminación global, etc.
En infografía este proceso se desarrolla con el fin de imitar un espacio 3D formado por
estructuras poligonales, comportamiento de luces, texturas, materiales, animación, simulando
ambientes y estructuras físicas verosímiles, etc. Una de la partes más importantes de los
programas dedicados a la infografía son los motores de render los cuales son capaces de
realizar técnicas complejas como radiosidad, raytrace (trazador de rayos), canal alpha,
reflexión, refracción, iluminación global, etc.
3.2 "Visualización de objetos"
El proceso de visualización 3D consiste en todas las operaciones que conlleva el despliegue de un objeto tridimensional en un dispositivo gráfico de salida. Por lo general, el objeto es concebido como una serie de triángulos, que serán procesados por un motor gráfico 3D, con soporte de hardware gráfico. El pipeline puede dividirse a alto nivel en 7 módulos:
a) PROCESADOR DE VÉRTICES:
Desde el punto de vista geométrico, este módulo transforma los vértices de la geometría al espacio de clipping. Además, realiza transformaciones sobre los atributos del vértice, como por ejemplo, la transformación del color, transformaciones de las coordenadas de textura y aplicación de un modelo de iluminación.
b) ENSAMBLAJE DE PRIMITIVAS:
En esta etapa se agrupan los vértices en primitivas para pasar a la siguiente etapa.
c) CULL, CLIPPING, VIEWPORT :
El culling consiste en remover las primitivas traseras o frontales de objetos. El clipping significa en este caso la remoción de primitivas o de partes de primitivas que no son visibles por el ojo. El espacio de clipping puede ser pensado como el espacio de ojo, en donde las se verifican si las primitivas gráficas están dentro, fuera o parcialmente dentro de la pirámide truncada de visualización. Sin embargo, 4 de los planos de la pirámide truncada son planos arbitrarios, por lo que el proceso de clipping en este espacio suele ser tedioso. Por ello, se trabaja en un espacio de clipping cúbico, en donde la pirámide truncada es transformada a un cubo de lado 2, delimitado por los puntos (-1,-1,-1) y (1,1,1). Es este espacio, la verificación de contención de primitiva es más manejable tanto el software como en hardware. La primitiva puede ser removida parcialmente, en cuyo caso, puede reducirse a una o varias primitivas, en donde nuevos vértices pueden ser creados, interpolando atributos de otros vértices. Estas primitivas son transformadas a coordenadas de dispositivo o viewport, para ser discretizadas por el módulo de rasterización.
d) RASTERIZACIÓN:
Es la conversión de las primitivas geométricas en fragmentos. Cada fragmento es una unidad discreta dentro del triángulo, y se corresponde con a un píxel del buffer de la imagen (framebuffer). Aquí se interpolan los colores resultantes en los vértices, para obtener el color inicial del fragmento.
Similarmente, se interpolan los valores de profundidad para el z-buffer, coordenadas de textura, y demás atributos que serán utilizados en los operadores por el procesador de fragmento. Debido a que el fragmento puede ser modificado e incluso eliminado en los módulos siguientes, aún no se le denomina píxel. La salida de este módulo son los datos asociados al fragmento, como color, coordenadas de textura, valor de profundidad, etc., todos obtenidos por interpolación.
e) PROCESADOR DE FRAGMENTOS:
Este módulo combina el color con la textura y demás propiedades del fragmento, para actualizar su color. La salida principal de este módulo es una tupla de color RGBA y una profundidad.
f) OPERADORES POR FRAGMENTO:
Antes de almacenar el fragmento en el buffer de la imagen, una serie de operaciones, incluso su eliminación, pueden ser aplicados. El fragmento puede ser eliminado si es muy transparente o no es visible o no forma parte de la máscara del esténcil. Si el fragmento pasa estas pruebas, la operación de mezcla o blending puede ser utilizada para mezclar el color del fragmento con el ya almacenado en la imagen, y además, podría aplicarse alguna operación lógica o de máscara de bits sobre su color.
g) OPERACIONES SOBRE LA IMAGEN:
Estas operaciones incluyen la inicialización o borrado de la imagen, así como la selección del buffer a utilizar, para el caso de doble buffer o estereoscopía.En la actualidad, las tarjetas gráficas soportan múltiples unidades para procesar vértices y fragmentos, para acelerar el tiempo de respuesta. Adicionalmente, estas unidades son programables en alto nivel, siendo muy populares los compiladores de CG (C for Graphics) y GLSL (Shading Language de OpenGL®). Estos transforman el código fuente escrito en C a código ensamblador entendible por las unidades programables.
3.3 TRANSFORMACIONES
TRIDIMENSIONALES
EXISTEN 5 TRANSFORMACIONES BÁSICAS LAS CUALES SON:
3.4 LINEAS Y SUPERFICIES CURVAS
La necesidad de representar curvas y superficies proviene de modelar y representar objetos reales o ficticios.
Normalmente no existe un modelo matemático previo del objeto, y el objeto se aproxima con “pedazos” de planos, esferas y otras formas simples de modelar cercanos a los correspondientes puntos del objeto.
Definiciones Básicas
Una curva es una línea continua de una dimensión, que varía de dirección paulatinamente.
Normalmente no existe un modelo matemático previo del objeto, y el objeto se aproxima con “pedazos” de planos, esferas y otras formas simples de modelar cercanos a los correspondientes puntos del objeto.
Definiciones Básicas
Una curva es una línea continua de una dimensión, que varía de dirección paulatinamente.

Una superficie es una extensión en que se consideran sólo dos dimensiones.
SUPERFICIES CURVAS
Las superficies curvas pueden generarse a partir de un conjunto funciones matemáticas que definen la superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario.
Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y gráfica posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones.
La definición analítica de una dada curva puede hacerse de varios modos y se relaciona directamente con la forma de representarla gráficamente:
- Explícitamente :
y = f(x)
- Implícitamente:
f(x, y) = 0
- Paramétricamente:
x = x(t)
y = y(t)
Representación Explícitay = y(t)
Es la mas conocida desde que nos ensenaron a utilizar las coordenadas cartesianas para graficar funciones.
En 3D, para representar una curva se requieren dos ecuaciones:
y = f (x), z = g(x)
Obteniendo una superficie en 3D que será:
z = f (x, y)
Representación Implícita
Para curvas y superficies estándar (rectas, círculos, planos, toroides, etc.), este tipo de definición es mas directa y permite visualizar y modificar sencillamente parámetros importantes y específicos de cada curva (radio en un circulo, distancia al origen en un plano, etc.).
En 3D, una superficie se describe por
f(x, y, z) = 0
Ejemplo
• Una esfera: x2 + y2 + z2 – r2 = 0
• Una curva corresponde a la intersección de dos superficies:
f(x, y, z) = 0 y g(x, y, z) = 0
Nota: el punto (x, y, z) debe pertenecer a ambas superficies.
Representación Paramétrica
El valor de cada variable espacial se expresa en términos de una variable independiente (t), llamada parámetro.
Estas funciones juntas han de formar las ecuaciones paramétricas de una curva:
x = x(t)
y = y(t)
z = z(t)
Cada valor de t determina un punto (x,y) que se puede representar en un sistema de coordenadas.
Superficie Paramétrica al conjunto de puntos (x,y,z,) dados por r(u,v)= x(u,v)i + y(u,v)j + z(u,v)k.
Las Ecuaciones x=(u,v), y=(u,v) y z=(u,v) se llaman Ecuaciones Paramétricas de la superficie.
CONCLUSIÓN
Es muy importante tener un buen hardware para poder lograr tener la mejor calidad de imagen posible.
Esto no es muy independiente del software ya que en conjunto se logra tener una imagen lo más parecido a la realidad. Existen diversas técnicas de Creacion, Visualización y de Manipulación sobre la proyección de la imagen, esto es muy útil porque acelera la proyección de las imágenes haciendo que las partes del objeto que no son visibles en la pantalla preferentemente no se dibujen para que la velocidad de respuesta sea óptima.
No solo acelera el proceso ya que nos permite solo observar lo que necesitamos e irse actualizado en el momento de rotar la imagen.
BIBLIOGRAFIA
http://anahigraficacion.blogspot.mx/2013/10/32-visualizacion-de-objetos.html
http://graficacionz0r3th.blogspot.mx/2013/10/32-visualizacion-de.html
http://graficacion-suirot18.blogspot.mx/2013/10/31-representacion-de-
http://graficacion-suirot18.blogspot.mx/2013/10/31-representacion-de-

.jpg)





















No hay comentarios:
Publicar un comentario